Resistor Ladder calculation

[AdrianUK]

I know this is a little outside the scope of this forum, but I also know that some of the members here have an electronics/maths background.

I'm trying to understand how to analyse the resistor network below (this is not a homework problem - I'm way to old for that! It is a real world/project problem).

What I'm looking for is the method to calculate the voltages across R1, R2, R3, R4, R5 & R6.

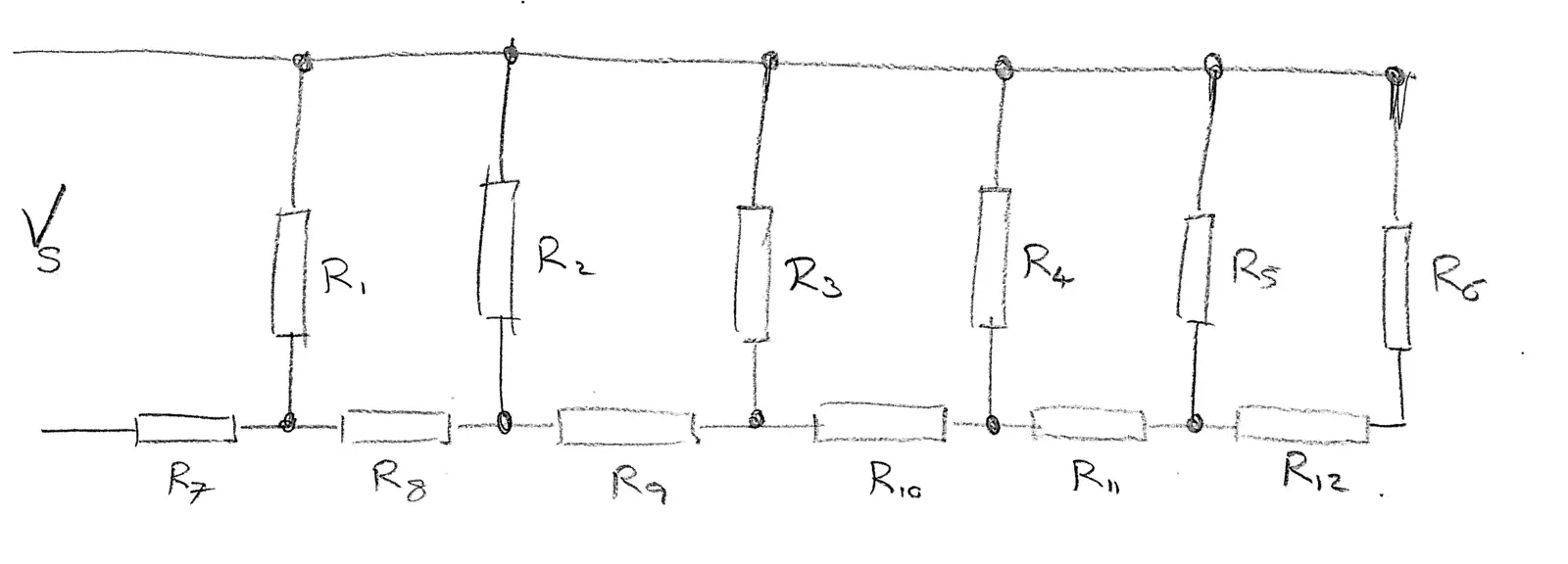
Lets assume that all the resistances are different. Obviously this can't be done by simply combining the resistors since the currents through R7, R8... R12 etc will all be different.

So how is it done? As I said above, I'm not expecting anyone to do this for me, but pointers to a mathematical method would be great!

 

[bernardgreen]

Calculate the virtual resistor Rab using 1/Rab = 1/R5 + 1/(R6+R12)

Then calculate Rcd

1/Rcd = 1/R4 + 1/(Rab + R11)

Repeat along the ladder

 

[JohnW2]

He may have thought it 'obvious' (which it may be to you) but what Bernard described does not, in itself, give you the answers you want (the voltages across R1, R2, R3, R4, R5 & R6), so ...

.... having used Bernard's technique to go all the way 'back down the ladder' to the stage at which you have just two resistances in series across Vs, namely R7 and "Rx", where Rx is the effective resistance of all the resistors other than R7, then the voltage across Rx is

Vs x [Rx / (Rx + R7) ]

... so that, in the original ladder, that would be the voltage across R1.

You can then repeat that process, moving to the right, replacing Vs with the voltage calculated for the previous resistor (e.g. the voltage across R1 in order to calculate that across R2), and replacing Rx with Ry, that being the equivalent you calculated (per Bernard) for all the resistors to the right of (and including) the one of interest.

Hence, for example, if as above, you calculate the voltage across R1 as V_R1, then the voltage across R2 will be:

V_R1 x [Ry / (Ry+R8) ]

Where Ry is (per Bernard calc) the equivalent resistance of everything to the right of (and including) R2 (i.e. the equivalent of all of R2-R6 and R9-R12)

... and so on.

Kind Regards, John

 

[bernardgreen]

Between John and I you have the method.

I am a bit curious ..... is there no resistance in the top line ?

 

[SUNRAY]

Even if they are in both sides they can be lumped for calculation purposes. I did something similar for loudspeakers along the street for VE day (one of those silly 'expert audiophile ' conversations) but lumped the cable resistance. Did the rough calcs in my head then had to do them on paper/calculator to show the losses were not as great as he thought.

 

[BS3036]

While it wasn't the original question, if all that was wanted was the answer, the way I would do it is put the circuit into LT Spice and read off the answers.

 

[JohnW2]

While it wasn't the original question, if all that was wanted was the answer, the way I would do it is put the circuit into LT Spice and read off the answers.

So probably would I - but, as you say, that wasn't really the question we were asked!

Kind Regards, John

 

[BS3036]

While it wasn't the original question...

...that wasn't really the question we were asked!

Pardon me for trying to be helpful.

 

[JohnW2]

Pardon me for trying to be helpful.

I'm not sure how my repeating, and agreeing with, what you wrote makes your input any less helpful

 

[AdrianUK]

Between John and I you have the method.

Indeed I have. And thank-you both for your input.

I did realise that Bernard had pointed the way to be being able to calculate a series of virtual resistors & hence combine these to get an equivalent resistance for the network. I was starting to think about how then to work back calculating the voltages. I must admit that I hadn't thought about it as a series of voltage-dividers {R1/(R1+R2)} so that pointer from JohnW2 set me off along the right track.

I've started to code this into EXCEL and its seems to be working nicely ... I'll check it again tomorrow for typos & sillies in my 'coding'.

I am a bit curious ..... is there no resistance in the top line ?

In this version, no.

Let me explain a little more about what I'm doing. The application is a teaching aid to try & explain/demonstrate (some of) the issues with 'long' radial distribution circuits.

In this model the resistors R1 thru R6 will be lamps (Yeah, I know that a filament lamp doesn't behave exactly like a resistor, and have a constant resistance, but this drawback is more than offset by the fact that the brightness of the lamp is a very clear visual indication of the voltage across it). These lamps represent 'consumers'.

The resistors R7 thru R12 will be rheostats and these represent the length/cross-sectional area of the distributor. Making the value of these higher makes the distributor 'longer' or the cross sectional area 'smaller'.

Using this tool it is, I hope, possible to demonstrate such things as why increasing the cross sectional area of the distributor at the start of the line has a bigger effect on the voltage profile than, say, doing this in the middle or the far end.

This is a first pass basic teaching model. I know it glosses over a few things: In a real (single phase) distributor the volt drop would be shared between the phase & neutral conductors (hence there would be resistors in the top line). The real world situation would be even more complex since the distributor would almost certainly be 3 phase and the volt drop in the neutral more complex but lets start simple.

Thank-you again Gentlement.

 

[AdrianUK]

While it wasn't the original question, if all that was wanted was the answer, the way I would do it is put the circuit into LT Spice and read off the answers.

Indeed. But its not as much 'fun' and doesn't help with the understanding as much fun as doing it from scratch.

The EXCEL model I've built will allow me to change the value of the 'line' resistors && the supply voltage (as I'm sure LT Spice will). and, while of know of the existence of LTSpice, I've never actually used it (yet!)

 

[Harry Bloomfield]

What I'm looking for is the method to calculate the voltages across R1, R2, R3, R4, R5 & R6.

Cor, not done any of that since college.

 

[AdrianUK]

Cor, not done any of that since college.

Me neither, that was the problem!

 

[bernardgreen]

Designing teaching aids brings out the best or the beast in the educator.
Often the educator can learn as much from designing the aid as the students do when using aid.

 

[JohnW2]

.... Let me explain a little more about what I'm doing. The application is a teaching aid to try & explain/demonstrate (some of) the issues with 'long' radial distribution circuits.
In this model the resistors R1 thru R6 will be lamps (Yeah, I know that a filament lamp doesn't behave exactly like a resistor, and have a constant resistance, but this drawback is more than offset by the fact that the brightness of the lamp is a very clear visual indication of the voltage across it). These lamps represent 'consumers'.
The resistors R7 thru R12 will be rheostats and these represent the length/cross-sectional area of the distributor. Making the value of these higher makes the distributor 'longer' or the cross sectional area 'smaller'.
Using this tool it is, I hope, possible to demonstrate such things as why increasing the cross sectional area of the distributor at the start of the line has a bigger effect on the voltage profile than, say, doing this in the middle or the far end.

Fair enough.

Whilst the model you are using will illustrate the point you are wanting to demonstrate, returning to Bernard's point/question, in reality the increasing resistance of your distribution circuit as you move along it (i.e. as represented by your 'rheostats') would obviously exist in both 'the top line' as well as the bottom one.

However, as I said, I don't think that will detract significantly from what you are wanting to demonstrate. You could, if you wanted, extend Bernard's method (and then apply mine) to the situation in which there was also a series of resistors 'in the top line' equivalent to your R7 to R12.

Kind Regards, John