Maths puzzle four

[empip]

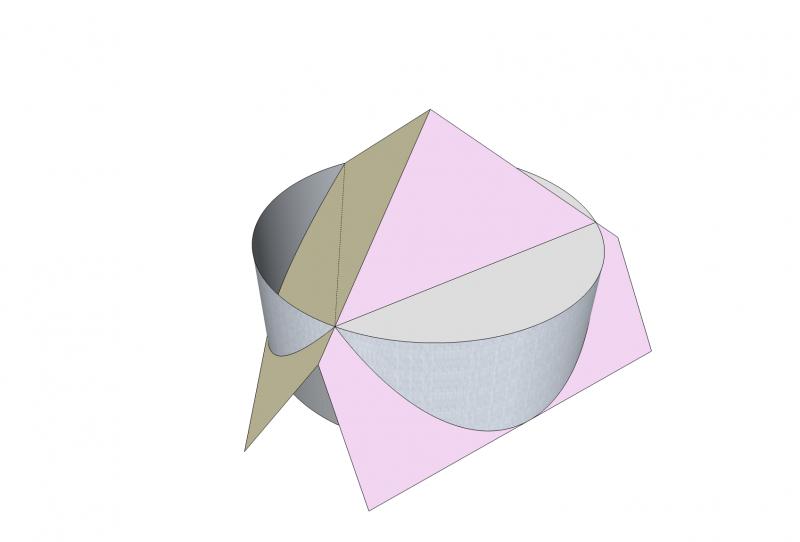
Guessing is not good - You need to picture the process, or using cad with solids capability add a solid cylinder to your solid cube, centre line coincident with the line between diametrically opposite cube corners.
The cylinder should be longer than the distance twixt cube corners in question.
Subtract the cylinder from the cube, interrogate the properties of the cube remaining read the volume. Compare to 1000 CC.

Calculating is a bit laborious but achievable without higher math.
Just need to picture the process. As the cutting tool eg. a flat ended milling cutter begins cutting the first peak of a corner 'pyramid' the resultant csa is triangular, as the cut progresses the triangle increases in length of side, then the cutter full diameter is cutting the three cube edges, the triangular csa is at a max - thus the base of pyramid in question.
As the cutter proceeds along it's path the csa begins growing radii propagating from what was the triangle corners.
when the growing radii come together and the cutter is working full face it will be machining a full cylinder until starting to break out from the sides at the opposite cube faces.
Need to calc. 'pyramid vol' x 2
From base of first pyramid to base of the second pyramid we can calc' a full cylinder, BUT we have the three 'fresh air' pockets (cylindrical wedges) as the cutter is approaching and entering full diameter cutting, these occur in the vicinity of both cube corners (http://mathworld.wolfram.com/CylindricalWedge.html)
So having calced this cylinder's vol including the wedges - If we subtract the volumes of the six wedges from the cylinder we have the material removed between the bases of the two pyramids add this to the vols of the pyramids and voila you have the volume removed.

-0-

 

[bernardgreen]

A lump of wood. a saw, a tape measure.

Create the cube,

Weigh the cube

Drill the hole.

Weigh the cube,

Calculate the percentage loss of weight

 

[Ian H]

Calculating is a bit laborious but achievable without higher math.

For it to loose 5% the diagonal would have to be around 64cm long which it isn’t.

Did you work it out with a 10mm radius? It should be 5mm and that’s why your answer is wrong.

 

[SammyInnit]

My brother managed to work it out. He does CNC programming.

The volume of the cube is 1000000mm and the cut out material is 13132.1mm so 1.3132% decrease.

However I can't show the working out.

 

[SammyInnit]

 

[Ian H]

He got the brains, you got the good looks

 

[SammyInnit]

He got the brains, you got the good looks

That's why I work out of a van and he works out of an office

 

[rsgaz]

My brother managed to work it out.

That's the best approximation we have so far, so, thanks to your brother for working it out, but it's still not the real answer Sammy.

That 'rod' that we're trying to remove from the cube won't have a cross on the end, it should look like a Mercedes badge from the 'end on' angle.

 

[SammyInnit]

That's the best approximation we have so far, so, thanks to your brother, but it's still not the real answer Sammy.

View attachment 153837

That 'rod' that we're trying to remove from the cube won't have a cross on the end, it should look like a Mercedes badge from the 'end on' angle.

It's not an approximation. It was put through a CAM simulation.

The cross on the 10mm 'rod' as you call it is the centrepoint of the cutter head signifying 10mm diameter. It's not an intersection of the material removed.

I'm sure I'd seen you post other screens from CAD software, surely you'd already have the answer if you're able to use it?

 

[rsgaz]

It's not an approximation.

It is if he thought the end of it had four facets rather than three, unfortunately. I want to know the answer too, damn you @EddieM

 

[SammyInnit]

It is if he thought the end of it had four facets rather than three, unfortunately. I want to know the answer too, damn you @EddieM

I asked him to simulate a 10x10x10 cm cube with a hole formed from point to point diagonally through the cube.

This is what he did and this is the answer it gave.

It's all 3D modelled and CAM simulated before sent to CNC, not 2D wireframe so he wouldn't have 'drawn' anything other than the cube in 3D.

I'm certain the 4 points are to show the 10mm bore centrepoint as you would expect to see with a 4 flue end mill typically used with a CNC 3axis cutter.

 

[EFLImpudence]

That is probably right, but the more I think about it, the more difficult it becomes.

This is a start,

but the corner, where the red lines meet, will be 120°, not 90°, wouldn't it?

The piece, until the drill is fully in, will be a three sided pyramid with the corners missing like this posted earlier.

Would it be the same, but easier to work out, if we were to imagine a triangular cutter, just pushed in (obviously couldn't rotate it), if the triangle had the same cross sectional area as the 1cm. diameter drill?
At least then we would have a perfect three sided pyramid of which we could calculate the volume.

 

[magicmushroom666]

This is how it looked for me:

 

[SammyInnit]

This is how it looked for me:
View attachment 153842

Yours has a mass of 9870xx, mine has the volume of 9868xx, that's a very tiny difference but I wonder why it exists.

 

[rsgaz]

will be 120°, not 90°, wouldn't it?

That IS modelled as 120°, like a Mercedes badge, but I wanted a side on view to add the red lines, which maybe doesn't show that all that well.

very tiny difference but I wonder why it exists.

Because of the four facets. That makes it too 'stubby'. If your brother can put that rod back into the model of the cube, you'll see that rod sticks out a bit now(not in a vertex to vertex way, that length is fixed) and is not flush with the original cube's edges. So you've minus-ed too much from the total volume.