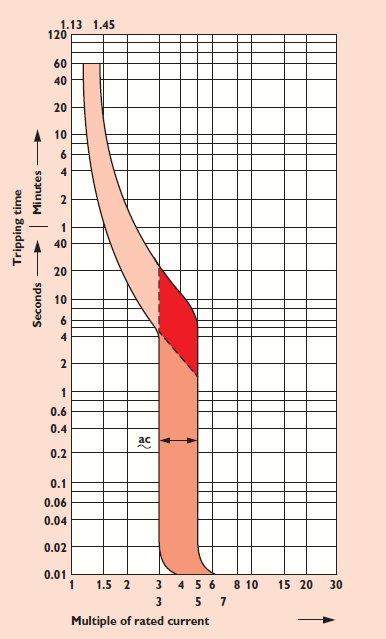
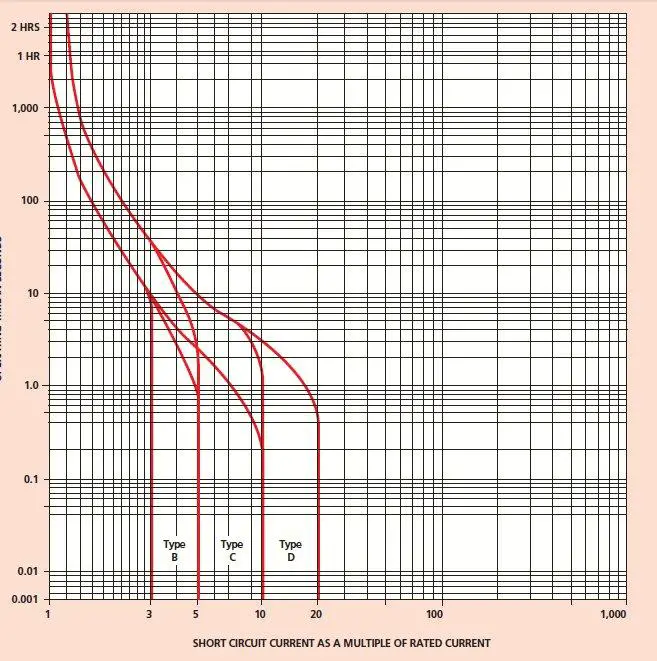
I presume the Hager curves are correct for Hager devices; others probably different.
Perhaps that is why, for the problem being discussed, there are no standard charts and advice is given to contact the manufacturer's figures.
What text is associated with the IET curve chart you gave?
I suspect it is formed from the calculations.
Perhaps that is why, for the problem being discussed, there are no standard charts and advice is given to contact the manufacturer's figures.
What text is associated with the IET curve chart you gave?
I suspect it is formed from the calculations.