Supplementary Bonding Revisited

[EFLImpudence]

I cannot get out of my head that the extraneous-c-p 'A' is merely a way of touching the exposed-c-p 'C' and MET , and so the toucher being subject to the Volt drop on the CPC during the fault, so looking at it this way:

Longer conductors with higher impedance would require bonding (in the absence of RCDs).

Therefore, if R2 (and extraneous-c-p) was sufficiently short to reduce the VD to a safe level (R<50/Ia) without SB, would that not explain the regulation?

 

[JohnW2]

[moved here from 'wrong thread]

I cannot get out of my head that the extraneous-c-p 'A' is merely a way of touching the exposed-c-p 'C' and MET , and so the toucher being subject to the Volt drop on the CPC during the fault, so looking at it this way:...

We seem to have 'jumped threads'

The end of the extraneous-c-p 'A' (which you have twisted around in comparison with my original diagram) does, indeed, provide a way of touching the MET - but definitely NOT the exposed-c-p-c 'C' (which is at a potential way above that of the MET).

By twisting part of my diagram around, you have not altered the fact that no current is flowing through the extraneous-c-p (from 'A' to MET) - hence no VD along it - so 'A' is at MET potential (whereas 'C' is at much higher than MET potential - so a large A-C PD).

Imagine your meter with one probe connected to the MET. If (with the fault), you put the other probe on 'C' (the 'live' exposed-c-p) you would measure a high voltage (~144V in my examples), but if you then moved that probe to 'A' (the 'far end' of the extraneous-c-p) you would measure zero voltage - do you not accept that? I suppose you'd better answer that before I try to go much further

Therefore, if R2 (and extraneous-c-p) was sufficiently short to reduce the VD to a safe level (R<50/Ia) without SB, would that not explain the regulation?

I don't really understand. "R2" (in both my diagram and your adaptation of it) is the CPC of the cable supplying the item with a fault, so can't be changed (by SB or anything else).

However, you may have gone some way to helping me to try to answer your question by saying " if R2 (and extraneous-c-p) was sufficiently short... ". Imagine reducing the length of the extraneous-c-p to zero, so what you were then touching would be the MET itself - and hopefully you will accept that "the MET is at MET potential"!

Then, rather than touching the MET directly, hold a 1 metre length of copper pipe and touch it's other end onto the MET - do you not accept that your hand will still be experiencing 'MET potential'?

If you do that, then change from a 1 metre length of copper pipe to a 20 metre long pipe (again, holding one end and touching the other onto the MET) - do you accept that your hand is still experiencing 'MET potential'?

Finally, put a 100kΩ resistor in the connection between pipe and MET - do you accept that your hand is still at 'MET potential'?,

If you accept that your hand would be experiencing 'MET potential' in all those scenarios, you ought to have convinced yourself that (because no current is flowing through it) if you have a conductor (an extraneous-c-p) connected to the MET at one end and connected to nothing (electrically) at the other end, then the 'far end' of that conductor will be at MET potential no matter what the length or resistance of the conductor.

Kind Regards, John

 

[EFLImpudence]

You seem to have forgotten that we are talking about a person touching A and C during a fault when many Amps are flowing through the MET.

I accept that no current is flowing in the extraneous-c-p in normal situations but there will be a little (and through you) when you touch A and C during a fault.

Yes the extraneous-c-p (or held pipe; that's what it is - a pipe with a bit of wire) is just an extension of your hand touching the MET.

So, do you not experience touch voltage (PD) dependent on the length of the CPC (R2) and Volt drop between C and MET during the fault?

 

[JohnW2]

You seem to have forgotten that we are talking about a person touching A and C during a fault when many Amps are flowing through the MET.

I haven't forgotten - and if you mean "when many Amps are flowing from C to the MET", then I agree.

I accept that no current is flowing in the extraneous-c-p in normal situations but there will be a little (and through you) when you touch A and C during a fault.

Indeed - but, as I said, that current 'through you' (and also 'through the extraneous-c-p') will be trivial (as I said, maybe a hundred mA or two, in comparison with the 'hundreds of amps' of fault current flowing through the CPC) - and certainly not enough to result in more than the most trivial of VD along the length of the extraneous-c-p (maybe a volt or three).

Yes the extraneous-c-p (or held pipe; that's what it is - a pipe with a bit of wire) is just an extension of your hand touching the MET.

Glad you agree!

So, do you not experience touch voltage (PD) dependent on the length of the CPC (R2) and Volt drop between C and MET during the fault?

Not the "length of the CPC". As I've explained, the main determinant of the voltage at C during a fault (i.e. the voltage between C and MET) is the ratio of the resistances of CPC and L-conductor in the cable. No matter how long (or short!) the CPC, the L-conductor will have the same length, and so that ratio will remain unchanged - e.g. 3:5 for 2.5/1.5mm² cable.

However, yes, since the extraneous-c-p remains at essentially MET potential (even when one is experiencing a shock), the 'touch voltage' (PD between extraneous- and exposed-c-ps) will, indeed, (during the fault) be "Volt drop between C and MET" [otherwise known as "the VD in/across the CPC (R2) ]- which, as I've said, will be roughly 144V for 2.5/1.5mm² cable (of any length).

You seem to be 'saying the right things' - so what is it that you are finding difficult to understand?

Kind Regards, John

 

[JohnW2]

Here's another "irony" for you to ponder ....

As you have said, to allow SB to be omitted, 701.415.2(vi), via 415.2.2, imposes a maximum, not minimum, on the resistance from extraneous-c-p to MET.

However, if that test is 'passed' (and the other conditions satisfied), hence SB not installed, then if one touches the extraneous-c-p at the same time as touching something 'live', then the higher the resistance of the extraneous-c-p (to MET), the lower will be the current passing though the victim of the shock.

In fact, a high extraneous-c-p (to MET) resistance can, in that situation, do one thing that an RCD can never do - namely limit the magnitude of shock that a person can experience (whereas all an RCD can do is the limit the duration)!

Thoughts?

Kind Regards, John

 

[EFLImpudence]

I don't know what else to say, except:

I think you are mixing up the situations of a person getting a shock by

a) touching a live part while simultaneously touching an earth.

and

b) touching two points on the same conductor while many Amps are flowing through it very briefly because of a fault - the shock being determined by the Volt drop on the conductor.

Is that not correct?

 

[JohnW2]

I don't know what else to say, except: .... I think you are mixing up the situations of a person getting a shock by
a) touching a live part while simultaneously touching an earth.
and
b) touching two points on the same conductor while many Amps are flowing through it very briefly because of a fault - the shock being determined by the Volt drop on the conductor.
.... Is that not correct?

No. Throughout the discussion, I have been talking exclusively about your (b) - provided we are agreed that the "same conductor" to which you refer is the CPC of the circuit in question - with the 'two points' therefore being the two ends of the CPC, one at the MET and the other at the exposed-c-p.

I certainly haven't ever been talking about (a). In that scenario, no amount of bonding will 'save' the victim from a ~230V shock - so their only hope of salvation is if a protective device limits the duration of shock to an extent that they don't die (unless they 'become disconnected').

In fact, in practical terms (i.e. from the victim's point-of-view), the only difference between your (a) and (b) is that [since there is no 'negligible impedance fault'] with (a) the victim will experience an ~230V shock, whereas in (b) it will be appreciably less (my ~144V for 2.5/1.5mm² circuit cable)[since there is a 'negligible impedance fault', resulting in VD in the L-conductor of the supply] .

Returning to (b), the place you have written "V=I x R" (adjacent to the connection between the exposed-c-p and the person's arm) perhaps gives some insight into the nature of the error in your thinking. The VD we are interested in (per your "the shock being determined by the Volt drop on the conductor.") is the VD in the circuit's CPC. The "I" is therefore the full PEFC (probably 'hundreds of amps') and the R is the resistance/impedance of the CPC - and, as above, your "I x R" should be around 144V with 2.5/1.5mm² circuit cable

I'm not sure what your "V = I x R" is meant to refer to, but (in terms of the shock) the above explains what it should refer to - and the current through the person (where you have actually written it) will be 'trivial' - hopefully no more that 100 - 200 mA at most.

Does any of that help?

Kind Regards, John

 

[EFLImpudence]

I'm not sure what your "V = I x R" is meant to refer to,

The Voltage through the person.

but (in terms of the shock) the above explains what it should refer to - and the current through the person (where you have actually written it) will be 'trivial' - hopefully no more that 100 - 200 mA at most.

...but that is not trivial.

Does any of that help?

No. I will have to bow out not understanding.

So, finally:
How is the reducing touch Voltage to <50V achieved as in the formula R = 50/Ia?

 

[JohnW2]

The Voltage through the person.

I presume you mean the voltage across the person? Do I therefore take it that the "I" in your "V = I x R" is the current through the person, and that the "R" is the resistance of that person's body?

...but that is not trivial.

In terms of the VD across (along the length of) any of the conductors we're talking about, 100-200 mA is totally trivial. Even if the resistance of the conductor were 5Ω (pretty unlikely), the VD would only be 0.5 - 1.0 V.

No. I will have to bow out not understanding.

Don't give up. It's actually very simple but we've all been there before and I am sure that once "the penny drops" you will wonder why it didn't drop 'years ago' ... and, apart from that, my selfish interest is that I would prefer not to have to live with the knowledge that my 'teaching skills' had failed

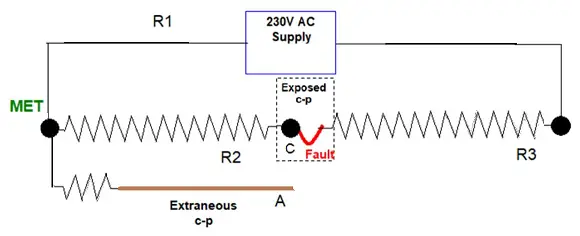
Let's try taking this in easy steps ...

I think you have accepted that in relation to the ('usual') type of L-E faults I have been discussing, the length and/or resistance of the extraneous-c-p are essentially irrelevant (provided, of course, that the resistance to MET is not so high as to mean that it does NOT qualify as an extraneous-c-p) - and that the extraneous-c-p is merely acting as a means of connection of a person to the MET. Do you agree?

If so, as you (maybe unwittingly!) suggested yourself, we can simplify the discussion by completely forgetting about the extraneous-c-p and, instead, assuming that the MET was conveniently placed (and touchable!) in the bathroom.

The 'touch voltage' (pd between the MET and the exposed-c-p which you are simultaneously touching) would then therefore simply be the potential difference between the exposed-c-p and the MET - which is the 'voltage drop across the resistance of the CPC when the fault current is flowing through it'.

Are you 'with me' so far? [I'll wait for an answer before continuing!]

So, finally: How is the reducing touch Voltage to <50V achieved as in the formula R = 50/Ia?

As I have said, I cannot make any sense of the implied suggestion that it does.

If the R one measures is (per 415.2.2) between the bathroom end of an extraneous-c-p and an exposed-c-p, then getting a result <50/Ia means one thing, and one thing only - namely that if a current of Ia were to pass through the entire path one had measured (from bathroom end of an extraneous-c-p to an exposed-c-p), then the potential difference between them would be <50V. Simply Ohm's Law.

However, as I've said, try as I may, I cannot think of any credible way in which such a situation could arise. How one earth could one end up with (or even 'contrive') a situation in which Ia was flowing through the entire path from bathroom end of extraneous-c-p to an exposed-c-p ???

In any other situation, R < 50/Ia (with R measured as described above) does not guarantee anything. In particular, as I have illustrated, in the face of the ('usual') type of L-E fault I have been talking about (and in the absence of SB), the potential difference between extraneous-c-p and exposed-c-p (which I presume is what you mean by 'touch voltage'?) can be considerably more than 50V, even if "R" is extremely small, far below 50/Ia.

Hence, as I asked at the start of this thread, exactly what does 415.2.2 things that it achieves?

Kind Regards, John

 

[SUNRAY]

I haven't been trying to follow the explanations so far but I see they have got quite involved.

I once demonstrated to an apprentice who was struggling with ohm's law and number crunching with this simple circuit:

It was very simply supplied from a 32A RCBO CEEform socket. A B10 MCB, a full 100m of 2.5mm² 3c flex, a batten holder with 40W bulb with a 32A switch directly across it, 2 multimeters.

It started with calculating the resistance of the cable from the chart, then measuring with a Robin tester.

With switch open; V1 showed 238V, V2 showed 127mV. I asked him to calculate the current and predict what would happen when the switch closed, his answer was 161A [factor of 10 out] and the MCB would immediately trip.

I then asked him to operate the switch; The light went off, V1 showed 24mV, V2 showed 115V and of course the MCB remained on.

Does this help at all?

 

[JohnW2]

... With switch open; V1 showed 238V, V2 showed 127mV. I asked him to calculate the current and predict what would happen when the switch closed, his answer was 161A [factor of 10 out] and the MCB would immediately trip. .... I then asked him to operate the switch; The light went off, V1 showed 24mV, V2 showed 115V and of course the MCB remained on.

Something is surely wrong there?

On the basis of the figures you show (I haven't checked your 7.4Ω figures), your apprentice was surely correct in saying that the current with the switch closed would be about 161A and that the MCB would therefore immediately trip? If one assumes that the supply voltage would remain at 238V, then I = 238/(0.74 x 2) = 160.8 A - i.e. what your apprentice said. On the basis of the V2 you measured with the switch closed, it seems that supply voltage fell to about 230V when you closed the switch and then I = 115/0.74 = 155.4 A

Who is missing what?

Kind Regards, John

 

[SUNRAY]

Something is surely wrong there?

On the basis of the figures you show (I haven't checked your 7.4Ω figures), your apprentice was surely correct in saying that the current with the switch closed would be about 161A and that the MCB would therefore immediately trip? If one assumes that the supply voltage would remain at 238V, then I = 238/(0.74 x 2) = 160.8 A - i.e. what your apprentice said. On the basis of the V2 you measured with the switch closed, it seems that supply voltage fell to about 230V when you closed the switch and then I = 115/0.74 = 155.4 A

Who is missing what?

Kind Regards, John

Talk about stating the ****ing obvious.
My envelope/notes of the day. The apprentice did his bits in a notebook as he [we] were were working through some college questions. On the day we did calculations/measurements on a number of random pieces of cable, I remembered the 100m drum of HO7 and now reading this more carefully reminds me we also played with a big drum of 12C SY.

My apologies.

 

[JohnW2]

Talk about stating the ****ing obvious. .... My envelope/notes of the day. The apprentice did his bits in a notebook as he [we] were were working through some college questions. On the day we did calculations/measurements on a number of random pieces of cable, I remembered the 100m drum of HO7 and now reading this more carefully reminds me we also played with a big drum of 12C SY.
..... My apologies.

Thanks for 'clarifying'/apologising! I'm not totally sure, but are you saying that it was actually 1,000 metres, rather than 100m, hence 7.4Ω (not 0.74Ω) per core (which would, as you say, make the current 10 times less than with the figures you posted) ?

However, beyond being a very basic application of Ohm's Law, I'm not too sure what point you were making (in the context of this thread)?

Kind Regards, John

 

[SUNRAY]

Thanks for 'clarifying'/apologising! I'm not totally sure, but are you saying that it was actually 1,000 metres, rather than 100m, hence 7.4Ω (not 0.74Ω) per core (which would, as you say, make the current 10 times less than with the figures you posted) ?

However, beyond being a very basic application of Ohm's Law, I'm not too sure what point you were making (in the context of this thread)?

Kind Regards, John

Hopefully the minimal info on the notes is obvious and I actually did the cable calcs to post here based on 100m [which we did do with a reel of HO7, then we moved onto the big drum which was 12 core or possibly 18 core, I can't remember if we installed L&Nx6 plus a common earth or L,N&Ex6 for sets of 6 stage lights. In other words I used the notes as an aid memoire rather than total detail, although the voltages quoted are read directly from it.

Yes I agree it was VERY basic ohms law which a second year apprentice was still struggling with.

I felt there is confusion on the 'risk factor' of earth to neutral voltage and i was trying to demonstrate how it can be 1/2 of supply voltage under short circuit fault conditions.

 

[JohnW2]

I felt there is confusion on the 'risk factor' of earth to neutral voltage and i was trying to demonstrate how it can be 1/2 of supply voltage under short circuit fault conditions.

That's essentially the point I have been trying to get over to EFLI, and I have a feeling that it's this point he's having some difficulty with.

The only difference in what I've been writing (and illustrating in diagrams) to him is that, since my examples have been based on 2.5/1.5mm² T+E that potential becomes 5/8 of supply voltage (rather than 1/2), relative to E/N, because of the differing CSAs of the L-conductor and CPC of such a cable (so the point of the fault would be at about 144V relative to E or N).

The point I've been trying to make in these discussions is that, with such a short from L to an exposed-c-p (hence also to the CPC), the potential difference between that exposed-c-p and the other end of the CPC (i.e. the MET) will be that 144V (or whatever), and so will the PD between that exposed-c-p and anything even vaguely connected to the MET (like an extraneous-c-p) also always be roughly that 144V.

The main problem is that the regs seem to be trying to imply that if the measured resistance from extraneous-c-p to exposed-c-p is less than a certain value, one can limit that potential difference to <50V - but, unless someone can prove me wrong, I think that's rubbish - since, per the above, in the scenario I'm talking about it seems to me that it will always be around 144V, regardless of any measured resistances!

Kind Regards, John